Математики, ваша помощь нужна. «Пятнашки»

cyber_Krosh, да правда что 50% не складываются, вот к примеру из википедии:

Можно показать, что ровно половину из всех возможных 1 307 674 368 000 (=15!) начальных положений пятнашек невозможно привести к собранному виду: пусть квадратик с числом i расположен до (если считать слева направо и сверху вниз) k квадратиков с числами меньшими i. Будем считать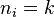 , то есть если после костяшки с i-м числом нет чисел, меньших i, то k=0. Также введем число e— номер ряда пустой клетки (считая с 1). Если сумма

является нечётной, то решения головоломки не существует.

(с) википедия

Т.е. Вам как я предполагаю нужно после рандома проверить если сумма получилось нечетной, то снова рандомить, пока сумма не будет четной

Упс пока писал опередили... но прочтите тогда идею решения

Можно доказать, что половину из всех возможных 15! начальных положений пятнашек невозможно собрать.

AlikZP, PerpetuumMobile, да, я тоже уже нашел.

Хороший сеошник, что тут скажешь...

Всем спасибо)

А может зарандомить алгоритм генерации начального положения из конечного?

Там же очень простой алгоритм получится:

выбираем из соседей пустой клетки любой (рандомно) квадратик и помещаем его в эту клетку....

И так 100500 раз....

Надо же никто сразу в Гугл не послал. Какие все добрые. :)

или сонные...

гугл в помощь!

ЗЫ: в дипломе математик, но я попячен)

Поздно .

гуглить не когда не поздно ;)

AlikZP:
Пятнашки представляют собой классическую задачу для моделирования эвристических алгоритмов. Обычно задачу решают через количество перемещений и поиск манхеттенского расстояния между каждой костяшкой и её позицией в собранной головоломке. Для решения используются алгоритмы наподобие алгоритма A*.

Нерешаемая комбинация, предложенная Ноем Чепменом

Можно показать, что ровно половину из всех возможных 1 307 674 368 000 (=15!) начальных положений пятнашек невозможно привести к собранному виду: пусть квадратик с числом i расположен до (если считать слева направо и сверху вниз) k квадратиков с числами меньшими i. Будем считать ni = k, то есть если после костяшки с i-м числом нет чисел, меньших i, то k = 0. Также введем число e — номер ряда пустой клетки (считая с 1). Если сумма



является нечётной, то решения головоломки не существует[2].

Для обобщённых пятнашек (с бо́льшим, чем 15, количеством костяшек) задача поиска кратчайшего решения является NP-полной.

Если допустить поворот коробки на 90 градусов, при котором изображения цифр окажутся лежащими на боку, то можно перевести неразрешимые комбинации в разрешимые (и наоборот). Таким образом, если вместо цифр на костяшки нанести точки и не фиксировать положение коробки, то неразрешимых комбинаций вообще не окажется.

Вики

PerpetuumMobile:
cyber_Krosh, да правда что 50% не складываются, вот к примеру из википедии:

Можно показать, что ровно половину из всех возможных 1 307 674 368 000 (=15!) начальных положений пятнашек невозможно привести к собранному виду: пусть квадратик с числом i расположен до (если считать слева направо и сверху вниз) k квадратиков с числами меньшими i. Будем считать , то есть если после костяшки с i-м числом нет чисел, меньших i, то k=0. Также введем число e— номер ряда пустой клетки (считая с 1). Если сумма



является нечётной, то решения головоломки не существует.

(с) википедия


Т.е. Вам как я предполагаю нужно после рандома проверить если сумма получилось нечетной, то снова рандомить, пока сумма не будет четной

Упс пока писал опередили... но прочтите тогда идею решения

Афигеть.😮